What is Reynolds number?
The Reynolds number is a parameter that describes the flow characteristics of a moving body of fluid. It is the ratio between the inertial forces and the viscous forces within a fluid and can be calculated using the equation below.
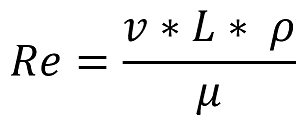
Where: υ = fluid velocity (m/s) L = characteristic length of the flow area (m) ρ = density of the fluid (kg/m³) μ = dynamic viscosity of the fluid (Ns/m²)
This dimensionless number has no direct physical meaning. However, it provides a useful insight into the behaviour of the fluid by characterizing the relative influence of both forces. Determining which force is dominant can predict whether the fluid is laminar or turbulent.
Laminar vs Turbulent flow
Every fluid has viscosity, or a tendency to resist flow. This is easy to visualize when pouring thick syrup from a bottle. At low Reynolds numbers, these viscous forces create a damping effect which results in a steady, orderly trajectory or Laminar flow.

At high Reynolds numbers, the inertia of the fluid is large enough to overcome its viscosity. Therefore, the flow becomes erratic and irregular, known as Turbulent flow.
To visualize the difference between laminar and turbulent flow, watch water pouring from a sink faucet. If you open the faucet slightly, it will produce a steady, clear stream of water, similar to laminar flow. Open it completely and you will see a nervous, uneven flow, similar to turbulent flow.
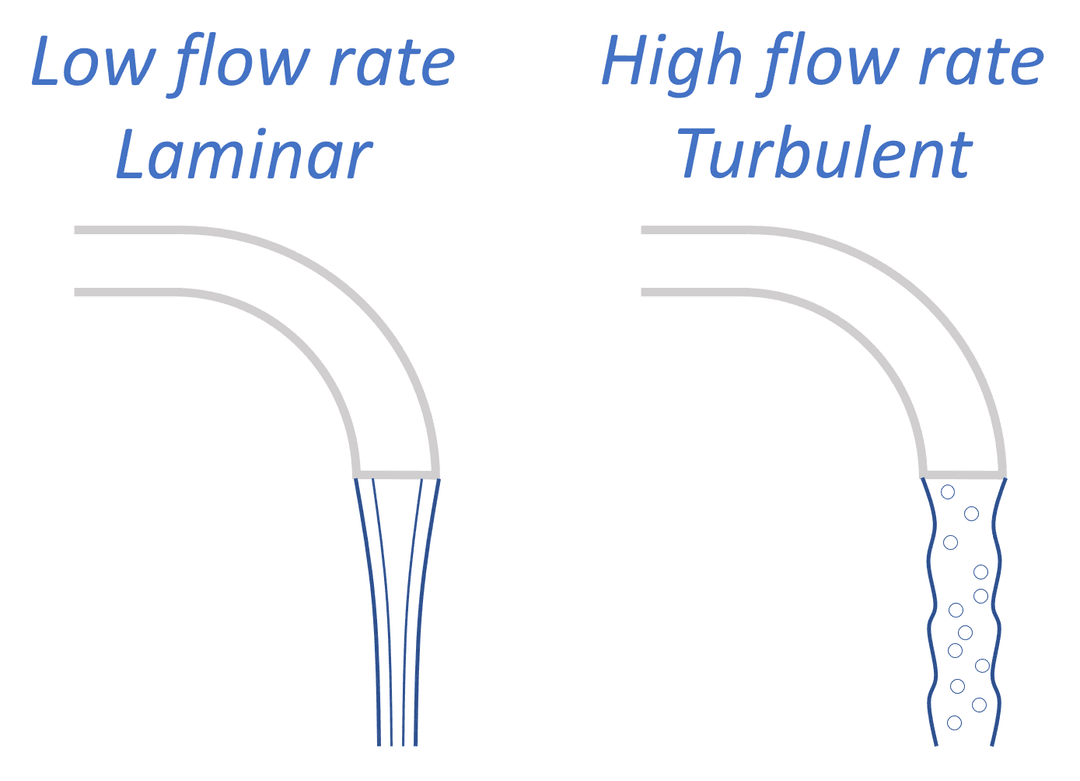
There is a range of Reynolds numbers where the flow is neither purely turbulent or laminar. Instead, it is in a transition state between the two. For flow in a circular pipe like the sink faucet, the flow regime is characterized by the following Reynolds number ranges:
-
Laminar Flow: Re < 2300
-
Transitional Flow: 2300 < Re < 4000
-
Turbulent Flow: Re > 4000
The importance of Turbulence
When designing any component subject to fluid flow, it is critical to understand whether the flow will be laminar or turbulent. Each regime has its own unique characteristics. For example, laminar flow, has less skin friction than turbulent flow. While turbulent flow mixes with the surrounding air and retains more kinetic energy, allowing it to stay attached to surfaces for longer.
The more complex an aerodynamic system, the more important it is to understand the operating flow regime. The size and shape of a component affects the characteristics of the air flowing around it. This can then affect the performance of other objects downstream.
Changing shapes
Calculating the Reynolds number can vary based on the shape of the object being analysed. The characteristic length in the Reynolds number equation describes the overall scale of the flow area being examined.
When fluid flows over an object, viscous forces slow down the molecules closest to the object's surface. This results in the relative velocity at the surface converging to zero and is referred to as a 'no-slip' condition. This layer of slower air between the surface and the free stream is called the Boundary Layer.
The larger the area the fluid flows over, the more space the boundary layer has to grow because more fluid is slowed down. Even when fluid flow begins as laminar, a critical point can be reached where the flow is destabilized and becomes turbulent.
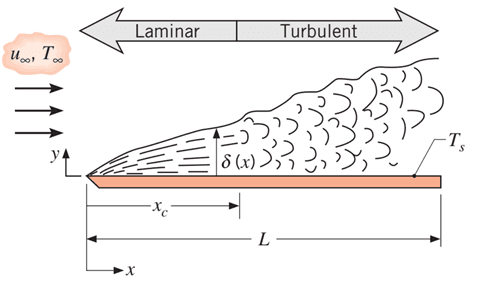
If all other variables (such as fluid density, viscosity, and velocity) are constant, then the characteristic length can be calculated for a given Reynolds number. Setting this equal to the transition zone between laminar and turbulent flow can be used to estimate a critical length. After which the flow will be turbulent.
This phenomenon can be experienced in real life by observing smoke rising from a candle. The smoke initially exhibits laminar flow, but after a certain height, begins to transition towards turbulence. All three flow regimes can be observed in the same wisp of smoke, so you can easily estimate the critical length of the flow.

Since fluid flow behaves differently around various shapes, no single universal definition of characteristic length exists. For example, the characteristic length for external flow around a flat plate is equal to the length of the plate. Whereas, for internal flow through a circular pipe, the characteristic length is defined as the inner diameter of the pipe.
Reynolds number in practice
The Reynolds number is not a real physical property, but rather a subjective method to characterize flow. It works best as a comparison tool instead of an absolute measure.
It is impossible to achieve perfect correlation between different aerodynamic tests unless they are carried out with identical conditions and procedures. This is why a constant Reynolds number is used between tests, to ensure the fluid is operating in the same flow regime. This is the most effective way to conduct an accurate comparison if it is impossible to exactly replicate the desired conditions.
Worked example: Wind Tunnel testing
Suppose you need to measure the lift and drag characteristics of a car at 40 kph to correlate with CFD simulations. However, the wind tunnel available is only large enough to accommodate a 1:3 scale model. By calculating the Reynolds number for the full car, you can then determine the air speed you need to conduct a representative wind tunnel test.

- Start by setting both Reynolds numbers equal:
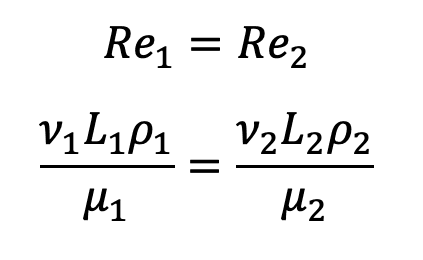
- Assuming the air density and viscosity remain constant, they cancel out leaving you with:
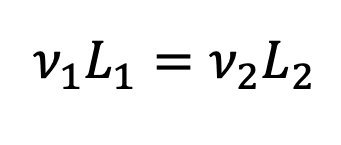
- Substitute the scale model length L2 in terms of the original length L1. Then you can calculate the required wind tunnel air speed to run the test:
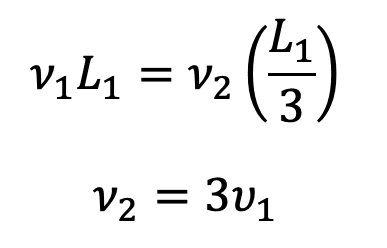
- Therefore, the air speed in the wind tunnel should be 120 kph. The lift and drag force generated can be used to calculate the lift and drag coefficient associated with that shape using the following formulas:
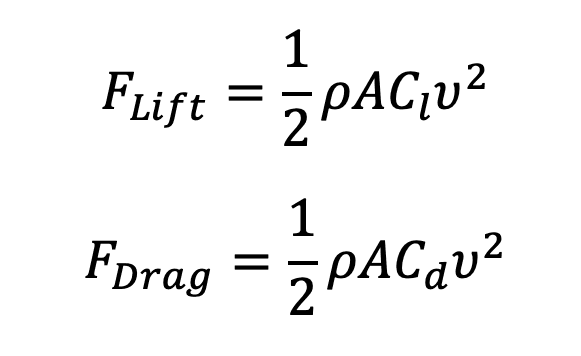
Where: ρ = air density (kg/m³) ν = velocity (m/s) A = reference area (commonly the frontal area) of the model (m) Cl = lift coefficient of the original vehicle Cd = drag coefficient of the original vehicle
Consistency is key
As the Reynolds number is not a physical parameter, consistency is extremely important when carrying out aerodynamic analysis. Published equations for characteristic length and turbulence transition range exist for a variety of shapes. But none of these will perfectly match the object you are analysing.
It is not always worthwhile to try and find the perfect definition of a value that has no direct physical meaning. Instead, it is best to pick a reasonable definition and stick to it. The consistency retained between data sets, the greater the validity of the Reynolds number as a tool for comparison and characterization. This consistency enables standardization on a global scale as we continue to push the frontiers of fluid dynamics.

