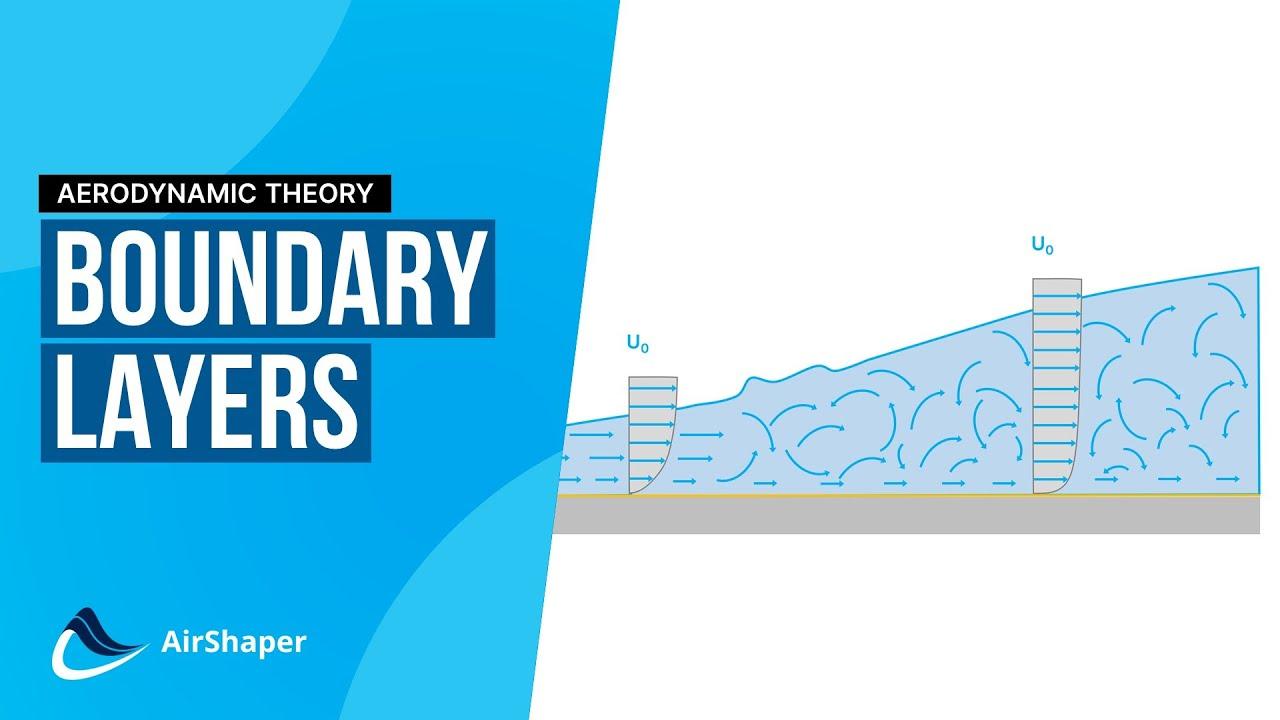
One of the most fundamental concepts to understand in fluid dynamics is the boundary layer. From golf balls to airplanes, boundary layers play a key role in optimising aerodynamic performance.
The 'no-slip' condition
When air flows over the surface of an object, the molecules closest to the surface stick to it, this is called the "no-slip condition" where the velocity at the surface is zero. The next layer of air above slows down due to the friction caused by colliding with the air molecules next to the surface. These slower moving molecules then collide with the next layer of air above and so on.
As you move further from the surface of the object, fewer molecules are affected by the collisions until the free stream velocity is reached. This is so far away from the object that the flow is completely undisturbed and so the velocity remains constant. This creates a thin layer of fluid near the surface where the velocity of the fluid changes from zero at the surface to the free stream velocity.
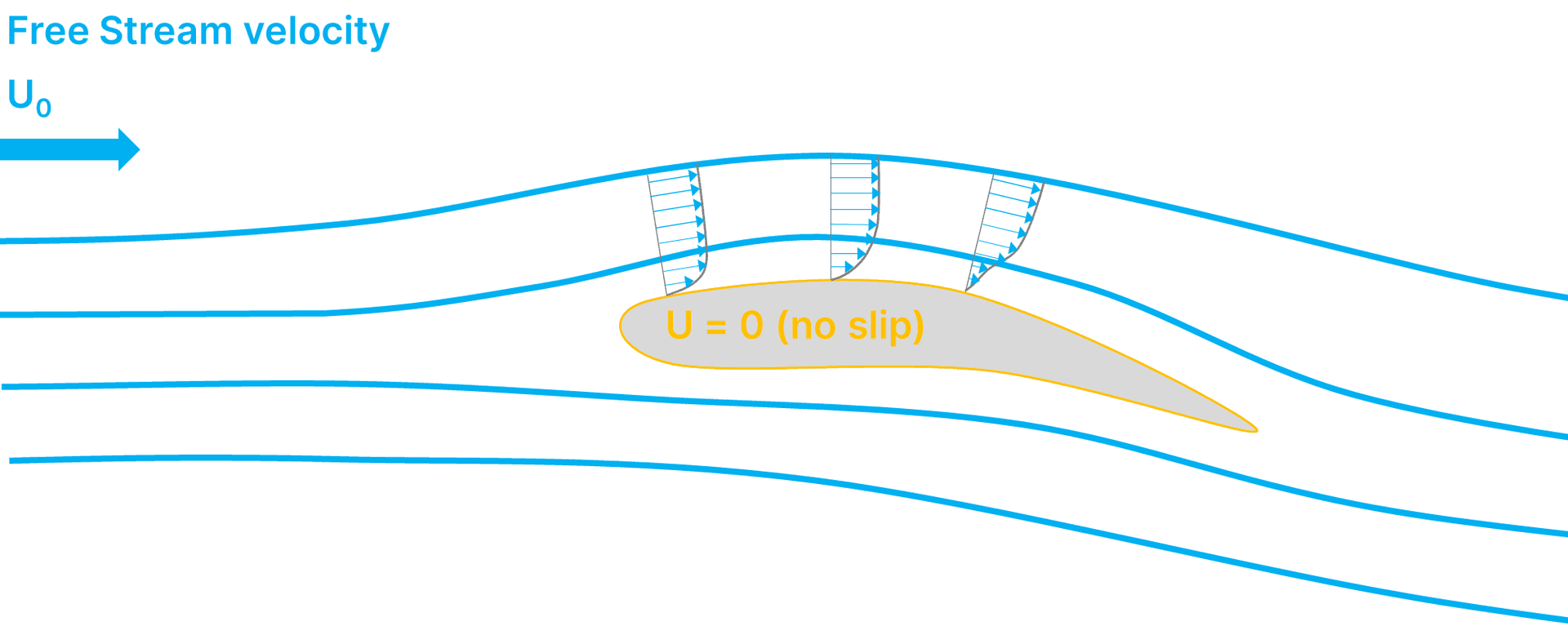
The boundary layer
Engineers call this thin viscous region of air flow the "boundary layer" and it is the main source of friction drag on an aerodynamic body. In most cases, the boundary layer is very thin compared to the rest of the flow, but it can have a significant effect on the aerodynamics downstream. For example, the friction drag on an Airbus 380 jumbo jet is generated by the boundary layer that wets the entire surface of the aeroplane in flight. So, this thin layer of air can have a huge effect on the overall aerodynamics.
A variety of concepts have been developed to try and minimise the drag caused by the boundary layer. One innovative solution is the STARC-ABL (single-aisle turboelectric aircraft with aft boundary layer). This features an all-electric BLI (boundary-layer ingesting) fan at the rear of the aircraft which sucks in the slow-moving boundary layer around the plane's body and converts it into additional thrust. This not only reduces drag, but NASA predicts that this design could result in fuel savings of up to 10%.

How the STARC-ABL concept works
Flow over a flat plate
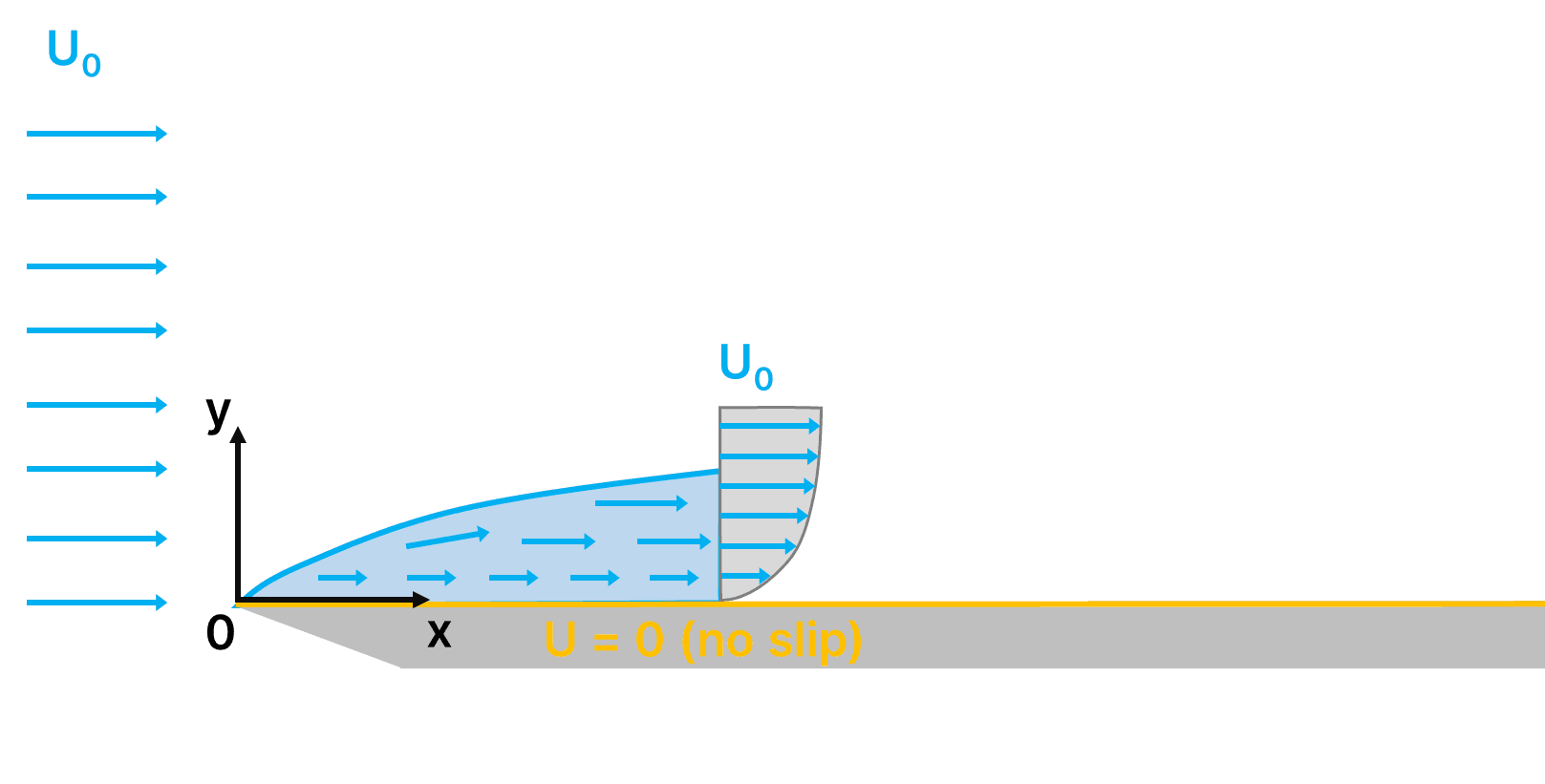
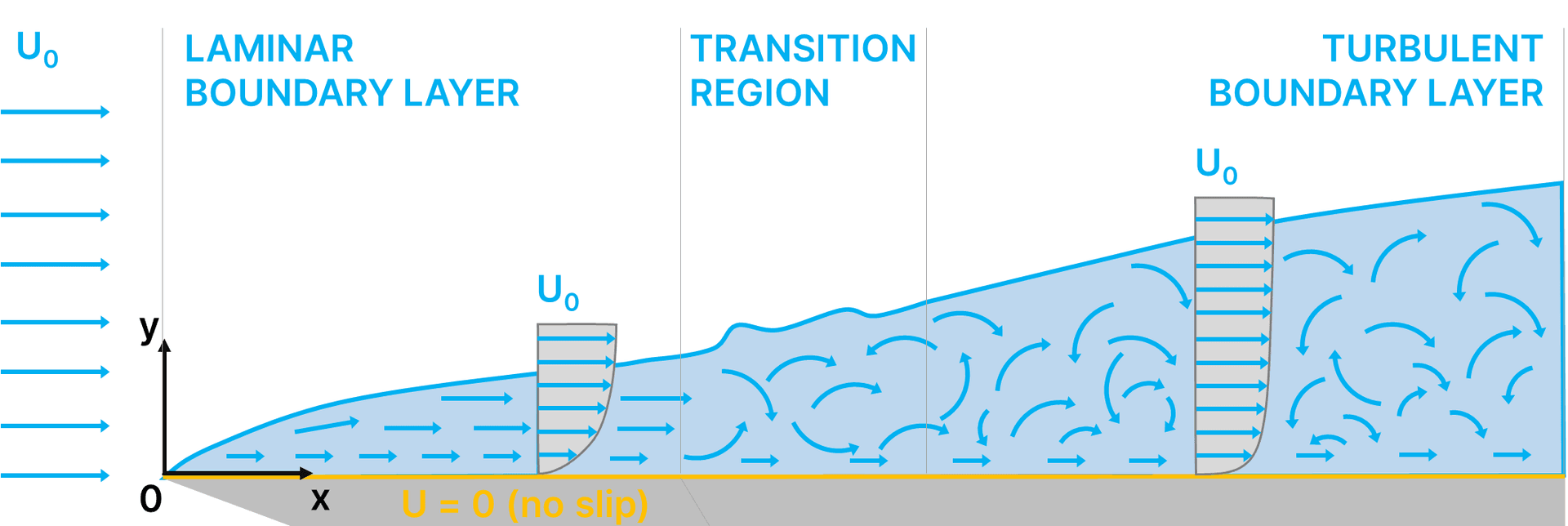
To fully understand the behaviour of the boundary layer, let’s look at air moving across a flat plate. As the undisturbed air meets the leading edge of the plate, the air molecules closest to the flat plate stick to it due to the no-slip condition. This slows down the layers of air closest to the surface, as explained above. As the air travels along the length of the plate, this layer of slower moving air, the boundary layer grows thicker.
Laminar vs Turbulent flow
The boundary layer can be broken up into two main categories; laminar or turbulent. When layers of air move parallel to the surface, this is called 'laminar' flow. Imagine adjacent layers of air sliding past one another like a deck of cards. In this regime, the primary source of drag is friction drag. This is caused by the physical amount of force the molecules of air are being slowed down by due to friction with the surface.
In a turbulent boundary layer, the boundary layer is filled with vortices featuring velocity variations in all directions. In contrast to laminar flow, the air no longer travels in layers and there is a rapid variation of pressure and flow velocity. In this regime, the predominant drag is pressure drag; the drag caused by a large drop in pressure.
In the example of the flat plate, if the oncoming airflow approaching the flat plate is laminar and there are no disturbances to trip the flow, the boundary layer will start off as laminar. As the air continues to move along the flat plate, the boundary layer will then transition to turbulent.
Reynolds number
The Reynolds number is an important dimensionless quantity used in fluid mechanics. It is often used to predict flow patterns in different flow conditions and can be used to predict the transition from laminar to turbulent flow. The exact definition of Reynolds number is shown below.
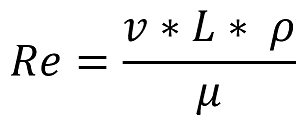
Where: υ = fluid velocity (m/s) L = characteristic length of the flow area (m) ρ = density of the fluid (kg/m³) μ = dynamic viscosity of the fluid (Ns/m²)
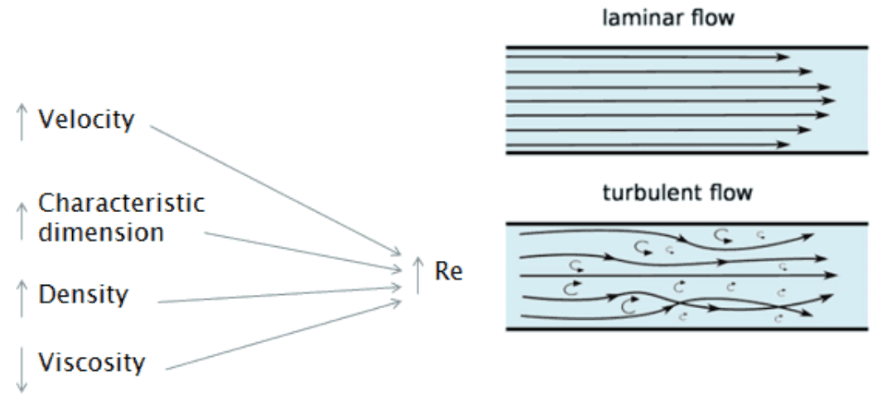
Basically, it is the ratio of inertial forces to viscous forces within a fluid. It is important to note that the Reynolds number changes with the "characteristic length". This is somewhat of an arbitrary expression but usually refers to the dimension that the air flows along. For an aerofoil it is usually the chord length, and for the example of the flat plate, it is the length along the flat plate.
Using this distance to calculate the Reynolds number, it is clear that the Reynolds number will increase as we move further down the plate. When the Reynolds number rises to a critical value, the laminar boundary layer transitions into a turbulent one.
Boundary layers in the real world
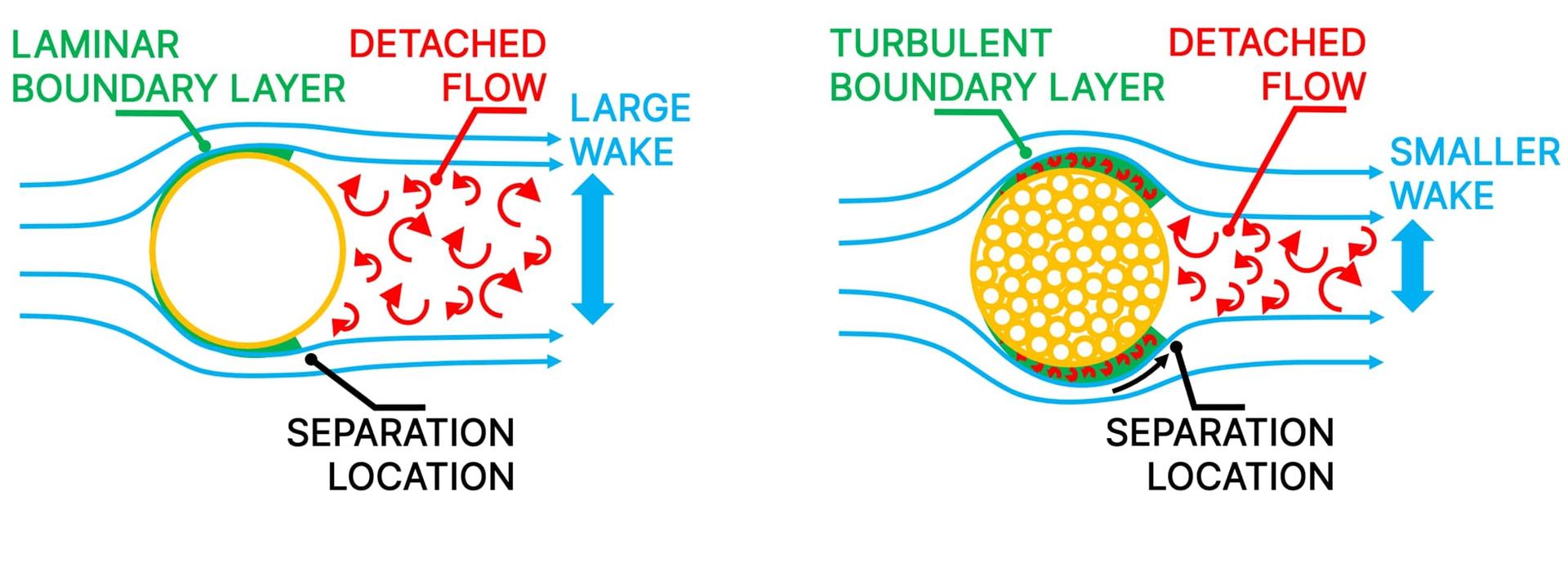
In applications like airplanes, boats, and high-speed trains, where shapes are smooth and streamlined, the goal is to maintain a laminar boundary layer as long as possible. A turbulent boundary layer is thicker than a laminar one, which increases the effective thickness and thus the pressure drag of the wing.
In applications with less streamlined shapes, like sports athletes or golf balls, it can be beneficial to trip the boundary layer and make it turbulent. Turbulent boundary layers carry more momentum and will push the separation point further downstream – that’s the reason golf balls have dimples and athletes wear special suits or even shin tape, reducing the wake they leave behind.