Aerodynamic drag is the force an object needs to overcome as it moves through air at a certain velocity.
So where does this force come from?
Aerodynamic drag
Air molecules are extremely small. On average there are around 26 quintillion (10^18) air molecules within a 1cm cube of air. When a solid object moves through air, it interacts with all these molecules generating millions of miniature forces.
Aerodynamic drag is the force needed to overcome these miniature forces when an object moves through air at a certain velocity. You can feel this force when you ride a bike. The faster you travel, the more air you have to push through and the higher your induced drag.
Even at speeds as low as 20km/h, over half the effort required to pedal a bike is due to overcoming aerodynamic drag. This is because the aerodynamic forces acting on a body increase with the square of velocity, as shown by the equation below.
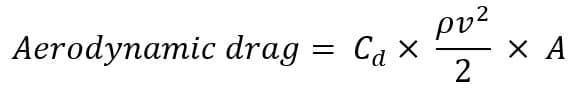
Where: Cd = drag coefficient ρ = density (kg/m³) v = velocity (m/s²) A = frontal area (m²)
If an object moves twice as fast, it will interact with twice as many air molecules within the same period of time. The impact with those molecules will also have twice the amount of energy. Therefore, the aerodynamic drag of an object increases substantially, even with a small increase in velocity
However, aerodynamic drag actually consists of two different components – pressure drag and skin friction drag. This is because a moving body experiences two types of forces:
-
Pressure forces acting normal to the object's surface
-
Friction forces acting tangential to the object's surface
Pressure drag
Pressure drag is the force acting perpendicular to an object’s surface. Consider a speed skier, as the skier travels down a slope, the air impacts the frontal area of the skier which builds up air pressure and consequently force. Air is also dragged along the skier’s surface, which reduces in pressure and creates a wake.
To calculate the aerodynamic drag of the skier, we first need to establish the total force, by integrating the pressure acting over the entire skier's surface. We then need to filter out the component of this force vector which is aligned with the wind.
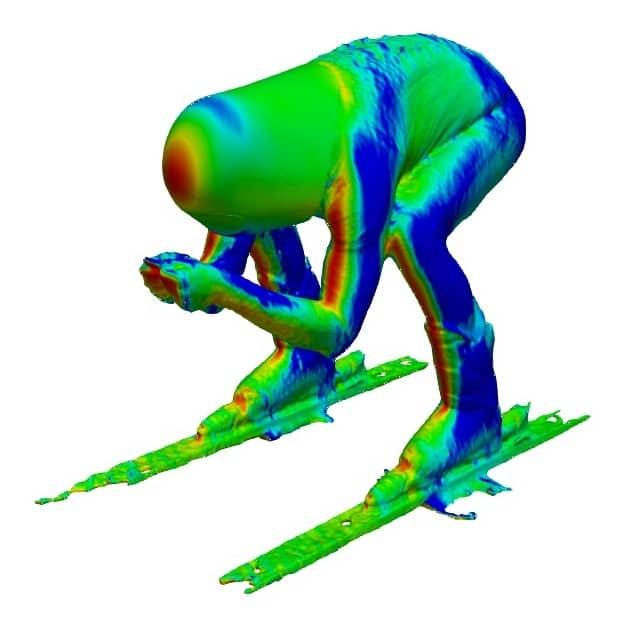
To identify which parts of the skier are contributing the most to drag, we need to look at local pressure. Clearly, the higher the pressure, the larger the contribution to drag. However, if the surface on which the pressure is acting is parallel to the direction of flow, then this has a minimal effect on pressure drag. However, if the surface on which the pressure is acting is perpendicular to the flow, such as the front of the helmet, then this will have a large effect on drag.
To visualise this, we’ve multiplied the local orientation of the surface with the local pressure to show the direct contribution of pressure drag below. Any surface which is perpendicular to the airflow shows a high contribution to drag, such as the helmet and hands. Whereas any surface which is parallel to the flow, does not contribute to drag at all.
Friction drag
Air also slides across the surface of an object, as it moves through a flow. This sliding action generates friction forces which act parallel to the object's surface, known as friction drag. Although typically friction drag is a much smaller contribution to aerodynamic drag than pressure drag.
In the case of the skier, friction drag only accounts for 4% of the total aerodynamic drag, as shown below.
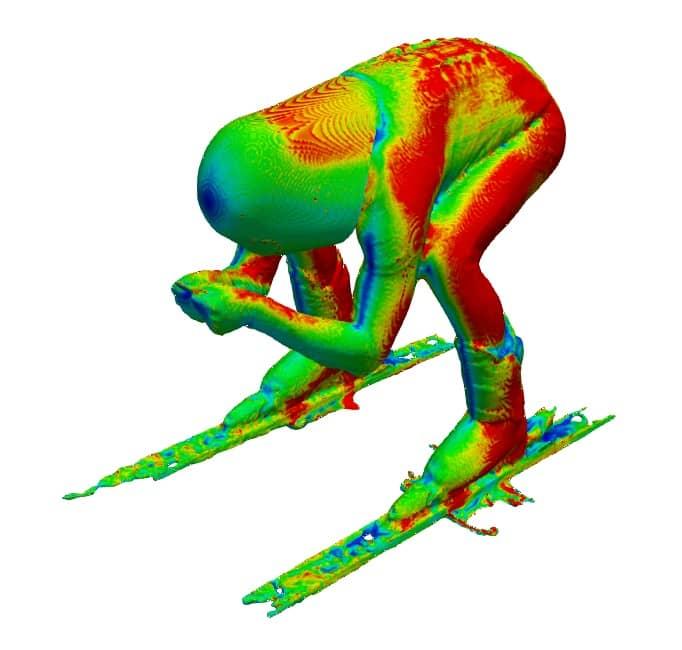
Forward-facing surfaces perpendicular to the flow, such as the helmet and hands have no friction drag at all. This is because air flowing perpendicular to an object decelerates to zero, known as the stagnation point, and therefore has no relative velocity. However, on the side of the skier, air has to speed up to travel round the curvature of these surfaces. This generates high local friction forces, resulting in friction drag.
Speed skiers are one of the many types of athlete who are now using CFD tools such as AirShaper to reduce drag and optimise aerodynamic performance.

